Biografias









- Bonsai(planta)
BONSAI Bonsai (japonês: ??, bon-sai) significa "árvore em bandeja" ou "árvore num vaso". Um bonsai precisa ter outros atributos além de simplesmente estar num vaso raso. A planta deve ser uma réplica de uma árvore da natureza em miniatura. Deve...
- Supercomputadores Gigantes
Supercomputadores Gigantes Assim é possível resumir as décadas de evolução da tecnologia computacional ? que tem desde monstruosidades a modelos leves, que cabem na palma da sua mão. E, apesar do uso dos computadores...
- Biografia-jean Bernard Léon Foucault(físico E Astrônomo )
Jean Bernard Léon FoucaultJean Bernard Léon Foucault (Língua francesa AFI: [??? b??na? le?? fuko]) (Paris, 18 de setembro de 1819 ? Paris, 11 de fevereiro de 1868) foi um físico e astrônomo francês .É mais conhecido pela invenção do pêndulo...
- O Que É Ano Bissexto?
Ano bissextoChama-se ano bissexto o ano ao qual é acrescentado um dia extra, ficando ele com 366 dias, um dia a mais do que os anos normais de 365 dias, ocorrendo a cada quatro anos (exceto anos múltiplos de...
- Biografia De Galileu Galilei
Galileu Galilei Nascimento e formação Filho de Vincenzio Galilei e de Giulia Ammannati di Pescia, nasceu em Pisa no dia 15 de Fevereiro de 1564. Os seus antepassados pertenciam à alta sociedade de Pisa e, embora a família tivesse decaído economicamente,...
Biografias
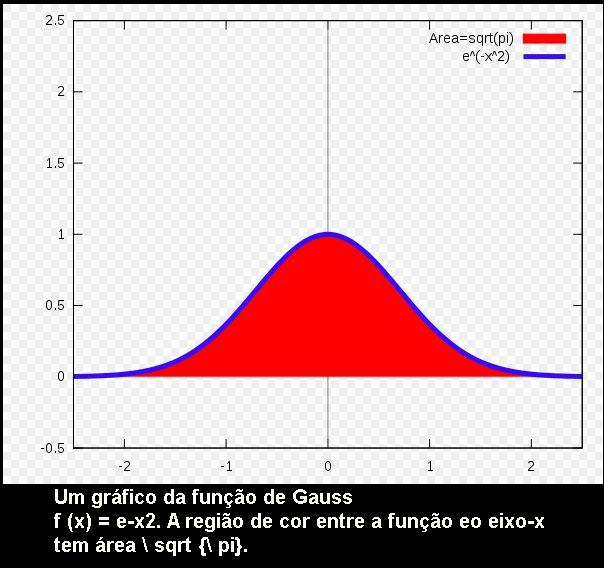
O QUE É NUMERO Pi?

| NUMERO PI Na matemática, o número  é uma proporção numérica que tem origem na relação entre o perímetro de umacircunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro é uma proporção numérica que tem origem na relação entre o perímetro de umacircunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro  e diâmetro e diâmetro 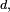 então aquele número é igual a então aquele número é igual a 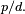 É representado pela letra grega ?. A letra grega ? (lê-se: pi), foi adotada para o número a partir da palavra grega para perímetro, "??????????", provavelmente por William Jones em 1706, e popularizada por Leonhard Euler alguns anos mais tarde. Outros nomes para esta constante são constante circularou número de Ludolph. É representado pela letra grega ?. A letra grega ? (lê-se: pi), foi adotada para o número a partir da palavra grega para perímetro, "??????????", provavelmente por William Jones em 1706, e popularizada por Leonhard Euler alguns anos mais tarde. Outros nomes para esta constante são constante circularou número de Ludolph.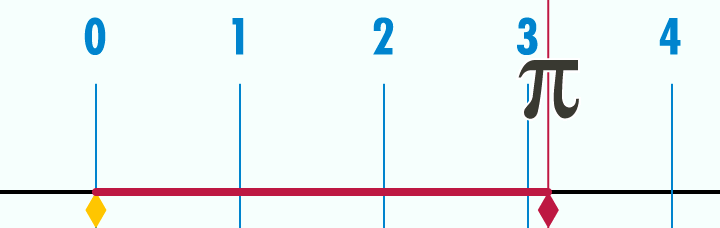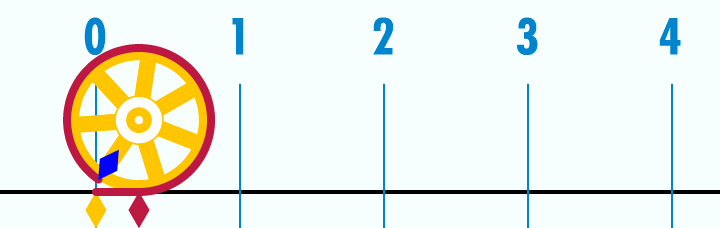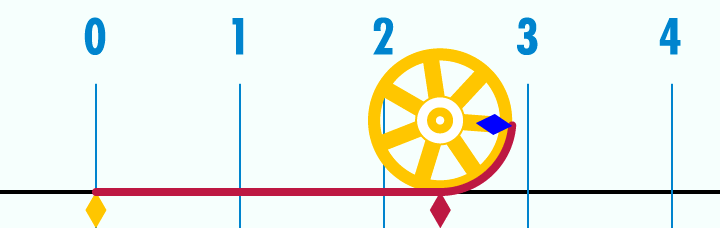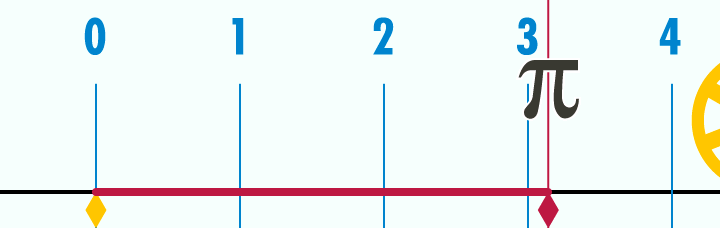 |
NotaçãoOs primeiros a utilizarem a letra grega  foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar definição atual1 foi William Jones. Entretanto foi só após Leonhard Euler utilizá-la que houve aceitação da notação pela comunidade científica. foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar definição atual1 foi William Jones. Entretanto foi só após Leonhard Euler utilizá-la que houve aceitação da notação pela comunidade científica. §Valor de |

Aproximações para |

Métodos de cálculoExistem muitas formas de se obter o valor aproximado de 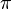 através de métodos numéricos. Consideramos que [[ através de métodos numéricos. Consideramos que [[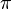 ]] é um número irracional e transcendente, de forma que os métodos de cálculo sempre envolvem aproximações, aproximações sucessivas e/ou séries infinitas de somas, multiplicações e divisões. ]] é um número irracional e transcendente, de forma que os métodos de cálculo sempre envolvem aproximações, aproximações sucessivas e/ou séries infinitas de somas, multiplicações e divisões.§Método clássico para o cálculo de |

O valor de 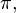 portanto, seria 3,1416. Obviamente, quanto maior o número de casas decimais, melhor a aproximação do valor real de pi. Mas devemos considerar que, na época, isso não era algo fácil de se calcular. portanto, seria 3,1416. Obviamente, quanto maior o número de casas decimais, melhor a aproximação do valor real de pi. Mas devemos considerar que, na época, isso não era algo fácil de se calcular.O maior cálculo de casas decimais até o século XV foi 3,1415926535897932 feito pelo matemático árabe Ghiyath al-Kashi. O matemático holandês Ludolph van Ceulen, no final do século XVI, calculou um valor de 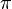 com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados. Por curiosidade, a sua esposa mandou gravar no seu túmulo o valor de com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados. Por curiosidade, a sua esposa mandou gravar no seu túmulo o valor de 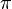 com as supracitadas 35 casas decimais. com as supracitadas 35 casas decimais.Hoje em dia é relativamente mais fácil, com os computadores modernos que calculam até bilhões de casas decimais para 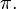 Uma aproximação de 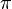 que apresenta diferença de aproximadamente 2,7e-7 é a seguinte: que apresenta diferença de aproximadamente 2,7e-7 é a seguinte:§ |

Formulação matemática do método de ArquimedesBaseado no método de Arquimedes é possível formular uma representação matemática para o cálculo de pi, eficiente para um polígono de qualquer número de lados. Considerando um polígono de n lados e raio 1, temos a medida do lado expressa pela lei dos cossenos: 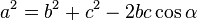 Temos formado um triângulo isósceles, de base l e lados r=1: 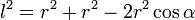 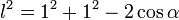 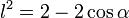  O ângulo do triângulo isósceles no centro do polígono é expresso por 360º dividido pelo número de lados (n), portanto: 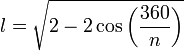 Dessa forma, o perímetro do polígono será de: 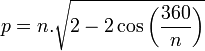 Como 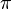 é representado pelo perímetro do polígono dividido pelo seu diâmetro, temos: é representado pelo perímetro do polígono dividido pelo seu diâmetro, temos: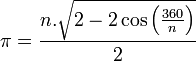 Aplicando transformações trigonométricas, a fórmula acima pode ser simplificada para: 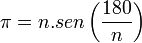 |

Métodos estatísticos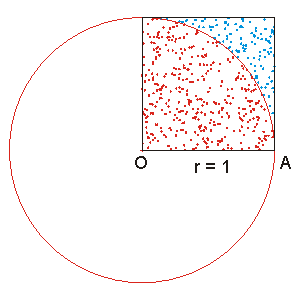 Outro método interessante para o cálculo de 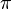 pode ser realizado através de Monte Carlo utilizando-se a estatística. Nesse método são sorteados aleatoriamente pontos num quadrado compreendido entre as coordenadas pode ser realizado através de Monte Carlo utilizando-se a estatística. Nesse método são sorteados aleatoriamente pontos num quadrado compreendido entre as coordenadas 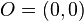 e e 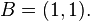 Em seguida calcula-se a distância dos pontos sorteados Em seguida calcula-se a distância dos pontos sorteados 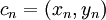 até a origem O = (0, 0). até a origem O = (0, 0). 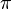 pode ser aproximado através do número de pontos inscritos na circunferência de raio 1 em relação ao total de pontos sorteados no quadrado de lado 1. pode ser aproximado através do número de pontos inscritos na circunferência de raio 1 em relação ao total de pontos sorteados no quadrado de lado 1.No exemplo ao lado , 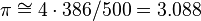 Outro método que utiliza a estatística de Monte Carlo para o cálculo de 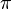 é conhecido como Agulha de Buffon, proposto no século XVIIIpelo naturalista francês Georges de Buffon. é conhecido como Agulha de Buffon, proposto no século XVIIIpelo naturalista francês Georges de Buffon. |

Métodos de séries infinitasO francês François Viète, estudando o método de Arquimedes, desenvolveu a seguinte série para o cálculo de 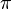 em 1593: em 1593:O matemático John Wallis, desenvolveu outra série infinita em 1655: Outra série conhecida para o cálculo de 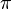 foi desenvolvida por Leibniz em 1682, utilizando-se da série de Taylor para a função arctan(x), tomando-se x=1 e, por conseguinte, arctan(1)= foi desenvolvida por Leibniz em 1682, utilizando-se da série de Taylor para a função arctan(x), tomando-se x=1 e, por conseguinte, arctan(1)=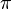 /4. /4.Johann Heinrich Lambert publicou, em 1770, uma série na forma de divisões infinitas: |

Métodos de cálculo numérico Um dos estudos dos métodos de cálculo numérico é obter a raiz de uma função. Quando consideramos a função 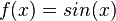 sabemos que sabemos que 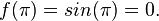 Os principais métodos do calculo numérico para a obtenção da raiz da função Os principais métodos do calculo numérico para a obtenção da raiz da função 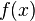 podem incluir uma busca binária no intervalo podem incluir uma busca binária no intervalo ![[a, b]](biografias/biografias-5643b499c47ad.png) onde se sabemos que onde se sabemos que 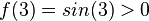 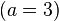 e e 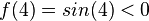 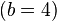 então podemos aprimorar o intervalo para: então podemos aprimorar o intervalo para:
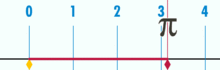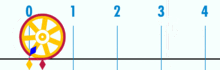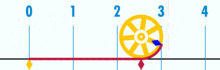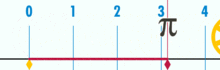
Partindo-se do intervalo ![\pi \in [3, 4]](biografias/biografias-5643b49c10e4e.png) esse método permite refiná-lo sucessivamente para os intervalos esse método permite refiná-lo sucessivamente para os intervalose assim sucessivamente. Ainda no cálculo numérico, o método de Newton-Raphson, mais eficiente que uma busca binária permite obter aproximações sucessivas para a raiz da função 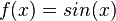 utilizando um ponto inicial utilizando um ponto inicial 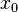 exigindo que conheçamos exigindo que conheçamos 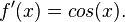 Tomando-se 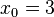 e considerando-se que por Newton-Rapson e considerando-se que por Newton-Rapsontemos a seguinte série para 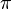 Um método otimizado de cálculo numérico para o cálculo de 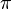 através das raízes de uma função pode ser obtido pela simplificação através das raízes de uma função pode ser obtido pela simplificaçãopois na proximidade de 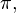 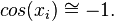 Notemos que nesses algoritmos de cálculo numérico considera-se 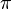 como trancendental, uma vez que a função como trancendental, uma vez que a função 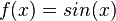 não pode ser escrita através de um polinômio finito de coeficientes racionais; a função não pode ser escrita através de um polinômio finito de coeficientes racionais; a função 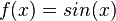 é obtida através da expansão da série de Taylor. é obtida através da expansão da série de Taylor. |
 |  |
Algoritmo de Gauss-LegendreO Algoritmo de Gauss-Legendre, que é um método de cálculo numérico de aproximações succesivas, foi utilizado por Yasumasa Kanada para obter o recorde mundial no cálculo de casas decimais de pi em 2002.12 §Método de cálculo isolado das decimais |
 |  |
Irracionalidade e transcendência de |


Cronologia do cálculo de |
| Matemático | Ano | Casas Decimais |
| Egípcios (Papiro de Rhind) | 1650 A.C. | 1 |
| Arquimedes | 250 A.C. | 3 |
| Zu Chongzhi | 480 D.C. | 7 |
| Ghiyath al-Kashi | 1424 | 16 |
| Ludolph van Ceulen | 1596 | 35 |
| Georg von Vega | 1794 | 126 |
| Gauss | 1824 | 200 |
| William Shanks | 1874 | 527 |
| Levi B. Smith, John W. Wrench | 1949 | 1.120 |
| Daniel Shanks, John W. Wrench | 1961 | 100.265 |
| Jean Guilloud, M. Bouyer | 1973 | 1.000.000 |
| Yasumasa Kanada, Sayaka Yoshino, Yoshiaki Tamura | 1982 | 16.777.206 |
| Yasumasa Kanada, Yoshiaki Tamura, Yoshinobu Kubo | 1987 | 134.217.700 |
| Chudnovskys | 1989 | 1.011.196.691 |
| Yasumasa Kanada, Daisuke Takahashi | 1997 | 51.539.600.000 |
| Yasumasa Kanada, Daisuke Takahashi | 1999 | 206.158.430.000 |
| Yasumasa Kanada | 2002 | 1.241.100.000.000 |
| Daisuke Takahashi | 2009 | 2.576.980.370.000 15 |
| Fabrice Bellard | 2010 | 2.699.999.990.000 16 |
| Shigeru Kondo & Alexander Yee | 2010/08/02 | 5.000.000.000.000 17 |
| Shigeru Kondo & Alexander Yee | 2011 | 10.000.000.000.000 18 |
| The Santa Clara University | 2013 | 8.000.000.000.000.000 19 |

loading...
- Bonsai(planta)
BONSAI Bonsai (japonês: ??, bon-sai) significa "árvore em bandeja" ou "árvore num vaso". Um bonsai precisa ter outros atributos além de simplesmente estar num vaso raso. A planta deve ser uma réplica de uma árvore da natureza em miniatura. Deve...
- Supercomputadores Gigantes
Supercomputadores Gigantes Assim é possível resumir as décadas de evolução da tecnologia computacional ? que tem desde monstruosidades a modelos leves, que cabem na palma da sua mão. E, apesar do uso dos computadores...
- Biografia-jean Bernard Léon Foucault(físico E Astrônomo )
Jean Bernard Léon FoucaultJean Bernard Léon Foucault (Língua francesa AFI: [??? b??na? le?? fuko]) (Paris, 18 de setembro de 1819 ? Paris, 11 de fevereiro de 1868) foi um físico e astrônomo francês .É mais conhecido pela invenção do pêndulo...
- O Que É Ano Bissexto?
Ano bissextoChama-se ano bissexto o ano ao qual é acrescentado um dia extra, ficando ele com 366 dias, um dia a mais do que os anos normais de 365 dias, ocorrendo a cada quatro anos (exceto anos múltiplos de...
- Biografia De Galileu Galilei
Galileu Galilei Nascimento e formação Filho de Vincenzio Galilei e de Giulia Ammannati di Pescia, nasceu em Pisa no dia 15 de Fevereiro de 1564. Os seus antepassados pertenciam à alta sociedade de Pisa e, embora a família tivesse decaído economicamente,...

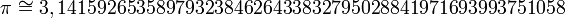 com 52 casas decimais.
com 52 casas decimais.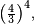 embora também seja encontrado o valor
embora também seja encontrado o valor 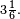 Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de
Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de 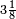 já ser conhecido como aproximação
já ser conhecido como aproximação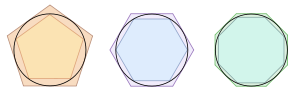
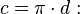
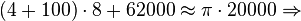
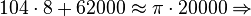
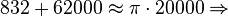
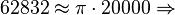
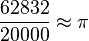
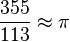
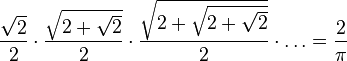
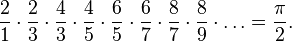
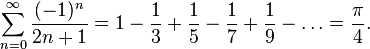
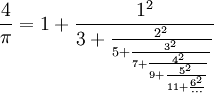
![[a, {{a+b} \over 2}],](biografias/biografias-5643b49af1667.png) se
se 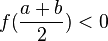 e
e![[{{a+b} \over 2}, b],](biografias/biografias-5643b49b89024.png) se
se 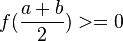
![\pi \in [3, 3.5]](biografias/biografias-5643b49c49984.png)
![\pi \in [3, 3.25]](biografias/biografias-5643b49c82114.png)
![\pi \in [3.125, 3.25]](biografias/biografias-5643b49cbab05.png)
![\pi \in [3.125, 3.1875]](biografias/biografias-5643b49d0fe66.png)
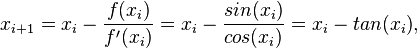
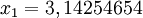
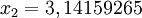
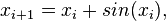
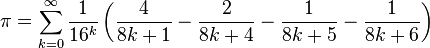
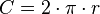
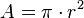
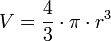
 é
é 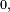 então nem
então nem 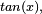 nem
nem 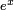 podem ser racionais . Como
podem ser racionais . Como 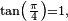 segue-se que
segue-se que 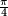 é
é  é irracional.
é irracional.